Having success at the Midnight Lump isn’t as easy as merely hurling a chunk of bait into the water. The pros have secrets that help them consistently deliver the goods.
Ask the average angler how wide an area his fish finder scans on the bottom at a depth of 30 feet, and your question will probably be met with a blank stare.It’s perfectly understandable. The shape of a fish finder’s transducer beam is regularly described with meaningless terms like wide, narrow and my personal favorite, effective. Some manufacturers pin the geometry down a bit with terms like 10- or 20-degree cone angle.
The beam of sound generated by a transducer starts out about the size of the transducer’s face and spreads at a fairly uniform rate on its way toward the bottom in a sort of cone-shaped pattern. Engineers have described the shape to me as being more elliptical than conical with side lobes protruding out around the transducer.
That’s all way too hard to understand, and since nearly anyone can picture an upside down ice cream cone with its point at the transducer and its open end on the bottom under the boat, the cone got voted in. Another engineer once explained to me that while a fish finder might see a wider area than the stated cone angle under ideal conditions, it would almost never see less area, so the cone shape was a safe bet.
Unfortunately there isn’t an absolute standard for calculating cone angles, which places them in the same gray area as electric trolling motor thrust. The closest thing to an industry standard for measuring cone angles is considering the point at which sound power drops by half to be the outside edge of the cone. If you hear a cone angle description like, “Twenty degrees at minus three db,” you can rest assured that the angle was measured using this standard because -3db or 3db down is techspeak for the half power point.
To visualize measuring a cone at its half power point, imagine yourself on the bottom of a lake under your boat with a sound meter and a wheelbarrow full of rocks. You walk around on the lake bottom under your transducer until you get the highest reading on the sound meter.
Sound is strongest in the center of the transducer’s beam, so you have located the center of your transducer’s cone. Park your wheelbarrow at that location. Now, take a rock out of the wheelbarrow and start walking in a straight line in any direction while watching your sound meter. When the meter reading drops to half of what it was at the wheelbarrow, stop and place the rock at that spot.
Next, go back to the wheelbarrow and pick up another rock. Walk in a straight line in another direction until the meter reading once again drops 50 percent, and place that rock on the spot.
Repeat this until you run out of rocks, and you will have an empty wheelbarrow in the center of a ring of stones that marks the outer edge of your transducer’s cone.
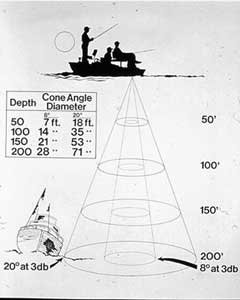
You can plot the shape of any cone angle on a sheet of paper with a ruler and a protractor, and then calculate the diameter of the cone at any depth, but it is much easier to use several rules of thumb. To measure the diameter of coverage of an 8-degree cone at any depth, simply divide that depth by 7. For instance, at a depth of 21 feet, the diameter of the circle of coverage would be 3 feet (21 divided by 7 equals 3).
To measure the diameter of the circle of coverage of a 20-degree cone, divide the depth by 3. For example, at the same 21-foot depth, a 20-degree cone covers a circle 7 feet in diameter (21 divided by 3 equals 7). The diameter of coverage of a 45-degree cone is equal to the depth, so a 45-degree cone would scan a circle 21 feet wide at our sample depth of 21 feet.
Wider cones find fish and large submerged structure features faster than smaller cones just like a floodlight finds something in the dark quicker than a spotlight.
Once found, you can zero in on your target to fish it more accurately with a smaller cone just like you can pinpoint a small object with that spotlight.


